In papers around volatility and cash (discrete) dividends, we often encounter the example of the flat volatility surface. For example, the OpenGamma paper presents this graph:
It shows that if the Black volatility surface is fully flat, there are jumps in the pure volatility surface (corresponding to a process that includes discrete dividends in a consistent manner) at the dividend dates or equivalently if the pure volatility surface is flat, the Black volatility jumps.
This can be traced to the fact that the Black formula does not respect C(S,K,Td-) = C(S,K-d,Td) as the forward drops from F(Td-) to F(Td-)-d where d is dividend amount at td, the dividend ex date.
Unfortunately, those examples are not very helpful. In practice, the market observables are just Black volatility points, which can be interpolated to volatility slices for each expiry without regards to dividends, not a full volatility surface. Discrete dividends will mostly happen between two slices: the Black volatility jump will happen on some time-interpolated data.
While the jump size is known (it must obey to the call price continuity), the question of how one should interpolate that data until the jump is far from trivial even using two flat Black volatility slices.
The most logical is to consider a model that includes discrete dividends consistently. For example, one can fully lookup the Black volatility corresponding the price of an option assuming a piecewise lognormal process with jumps at the dividend dates. It can be priced by applying a finite difference method on the PDE. Alternatively, Bos & Vandermark propose a simple spot and strike adjusted Black formula that obey the continuity requirement (the Lehman model), which, in practice, stays quite close to the piecewise lognormal model price. Another possibility is to rely on a forward modelling of the dividends, as in Buehler (if one is comfortable with the idea that the option price will then depend ultimately on dividends past the option expiry).
Recently, a Wilmott article suggested to only rely on the jump adjustment, but did not really mention how to find the volatility just before or just after the dividend. Here is an illustration of how those assumptions can change the volatility in between slices using two dividends at T=0.9 and T=1.1.
In the first graph, we just interpolate linearly in forward moneyness the pure vol from the Bos & Vandermark formula, as it should be continuous with the forward (the PDE would give nearly the same result) and compute the equivalent Black volatility (and thus the jump at the dividend dates).
In the second graph, we interpolate linearly the two Black slices, until we find a dividend, at which point we impose the jump condition and repeat the process until the next slice. We process forward (while the Wilmott article processes backward) as it seemed a bit more natural to make the interpolation not depend on future dividends. Processing backward would just make the last part flat and first part down-slopping. On this example backward would be closer to the Bos Black volatility, but when the dividends are near the first slice, the opposite becomes true.
While the scale of those changes is not that large on the example considered, the choice can make quite a difference in the price of structures that depend on the volatility in between slices. A recent example I encountered is the variance swap when one includes adjustment for discrete dividends (then the prices just after the dividend date are used).
To conclude, if one wants to use the classic Black formula everywhere, the volatility must jump at the dividend dates. Interpolation in time is then not straightforward and one will need to rely on a consistent model to interpolate. It is not exactly clear then why would anyone stay with the Black formula except familiarity.
Tuesday, November 25, 2014
Flat Volatility Surfaces & Discrete Dividends
In papers around volatility and cash (discrete) dividends, we often encounter the example of the flat volatility surface. For example, the OpenGamma paper presents this graph:
It shows that if the Black volatility surface is fully flat, there are jumps in the pure volatility surface (corresponding to a process that includes discrete dividends in a consistent manner) at the dividend dates or equivalently if the pure volatility surface is flat, the Black volatility jumps.
This can be traced to the fact that the Black formula does not respect C(S,K,Td-) = C(S,K-d,Td) as the forward drops from F(Td-) to F(Td-)-d where d is dividend amount at td, the dividend ex date.
Unfortunately, those examples are not very helpful. In practice, the market observables are just Black volatility points, which can be interpolated to volatility slices for each expiry without regards to dividends, not a full volatility surface. Discrete dividends will mostly happen between two slices: the Black volatility jump will happen on some time-interpolated data.
While the jump size is known (it must obey to the call price continuity), the question of how one should interpolate that data until the jump is far from trivial even using two flat Black volatility slices.
The most logical is to consider a model that includes discrete dividends consistently. For example, one can fully lookup the Black volatility corresponding the price of an option assuming a piecewise lognormal process with jumps at the dividend dates. It can be priced by applying a finite difference method on the PDE. Alternatively, Bos & Vandermark propose a simple spot and strike adjusted Black formula that obey the continuity requirement (the Lehman model), which, in practice, stays quite close to the piecewise lognormal model price. Another possibility is to rely on a forward modelling of the dividends, as in Buehler (if one is comfortable with the idea that the option price will then depend ultimately on dividends past the option expiry).
Recently, a Wilmott article suggested to only rely on the jump adjustment, but did not really mention how to find the volatility just before or just after the dividend. Here is an illustration of how those assumptions can change the volatility in between slices using two dividends at T=0.9 and T=1.1.
In the first graph, we just interpolate linearly in forward moneyness the pure vol from the Bos & Vandermark formula, as it should be continuous with the forward (the PDE would give nearly the same result) and compute the equivalent Black volatility (and thus the jump at the dividend dates).
In the second graph, we interpolate linearly the two Black slices, until we find a dividend, at which point we impose the jump condition and repeat the process until the next slice. We process forward (while the Wilmott article processes backward) as it seemed a bit more natural to make the interpolation not depend on future dividends. Processing backward would just make the last part flat and first part down-slopping. On this example backward would be closer to the Bos Black volatility, but when the dividends are near the first slice, the opposite becomes true.
While the scale of those changes is not that large on the example considered, the choice can make quite a difference in the price of structures that depend on the volatility in between slices. A recent example I encountered is the variance swap when one includes adjustment for discrete dividends (then the prices just after the dividend date are used).
To conclude, if one wants to use the classic Black formula everywhere, the volatility must jump at the dividend dates. Interpolation in time is then not straightforward and one will need to rely on a consistent model to interpolate. It is not exactly clear then why would anyone stay with the Black formula except familiarity.
It shows that if the Black volatility surface is fully flat, there are jumps in the pure volatility surface (corresponding to a process that includes discrete dividends in a consistent manner) at the dividend dates or equivalently if the pure volatility surface is flat, the Black volatility jumps.
This can be traced to the fact that the Black formula does not respect C(S,K,Td-) = C(S,K-d,Td) as the forward drops from F(Td-) to F(Td-)-d where d is dividend amount at td, the dividend ex date.
Unfortunately, those examples are not very helpful. In practice, the market observables are just Black volatility points, which can be interpolated to volatility slices for each expiry without regards to dividends, not a full volatility surface. Discrete dividends will mostly happen between two slices: the Black volatility jump will happen on some time-interpolated data.
While the jump size is known (it must obey to the call price continuity), the question of how one should interpolate that data until the jump is far from trivial even using two flat Black volatility slices.
The most logical is to consider a model that includes discrete dividends consistently. For example, one can fully lookup the Black volatility corresponding the price of an option assuming a piecewise lognormal process with jumps at the dividend dates. It can be priced by applying a finite difference method on the PDE. Alternatively, Bos & Vandermark propose a simple spot and strike adjusted Black formula that obey the continuity requirement (the Lehman model), which, in practice, stays quite close to the piecewise lognormal model price. Another possibility is to rely on a forward modelling of the dividends, as in Buehler (if one is comfortable with the idea that the option price will then depend ultimately on dividends past the option expiry).
Recently, a Wilmott article suggested to only rely on the jump adjustment, but did not really mention how to find the volatility just before or just after the dividend. Here is an illustration of how those assumptions can change the volatility in between slices using two dividends at T=0.9 and T=1.1.
In the first graph, we just interpolate linearly in forward moneyness the pure vol from the Bos & Vandermark formula, as it should be continuous with the forward (the PDE would give nearly the same result) and compute the equivalent Black volatility (and thus the jump at the dividend dates).
In the second graph, we interpolate linearly the two Black slices, until we find a dividend, at which point we impose the jump condition and repeat the process until the next slice. We process forward (while the Wilmott article processes backward) as it seemed a bit more natural to make the interpolation not depend on future dividends. Processing backward would just make the last part flat and first part down-slopping. On this example backward would be closer to the Bos Black volatility, but when the dividends are near the first slice, the opposite becomes true.
While the scale of those changes is not that large on the example considered, the choice can make quite a difference in the price of structures that depend on the volatility in between slices. A recent example I encountered is the variance swap when one includes adjustment for discrete dividends (then the prices just after the dividend date are used).
To conclude, if one wants to use the classic Black formula everywhere, the volatility must jump at the dividend dates. Interpolation in time is then not straightforward and one will need to rely on a consistent model to interpolate. It is not exactly clear then why would anyone stay with the Black formula except familiarity.
Tuesday, November 18, 2014
Machine Learning & Quantitative Finance
There is an interesting course on Machine Learning on Coursera, it does not require much knowledge and yet manages to teach quite a lot.
I was struck by the fact that most techniques and ideas apply also to problems in quantitative finance.
While it sounds like a straightforward remark, I have found that people (including myself) tend to do the same mistakes in finance. We might use some quadrature, find out it does not perform that well in some cases, replace it with another one that behaves a bit better, without investigating the real issue: why does the first quadrature break? is the new quadrature really fixing the issue?
I was struck by the fact that most techniques and ideas apply also to problems in quantitative finance.
- Linear regression: used for example in the Longstaff-Schwartz approach to price Bermudan options with Monte-Carlo. Interestingly the teacher insists on feature normalization, something we can forget easily, especially with the polynomial features.
- Gradient descent: one of the most basic minimizer and we use minimizers all the time for model calibration.
- Regularization: in finance, this is sometimes used to smooth out the volatility surface, or can be useful to add stability in calibration. The lessons are very practical, they explain well how to find the right value of the regularization parameter.
- Neural networks: calibrating a model is very much like training a neural network. The backpropagation is the same thing as the adjoint differentiation. It's very interesting to see that it is a key feature for Neural networks, otherwise training would be much too slow and Neural networks would not be practical. Once the network is trained, it is evaluated relatively quickly forward. It's basically the same thing as calibration and then pricing.
- Support vector machines: A gaussian kernel is often used to represent the frontier. We find the same idea in the particle Monte-Carlo method.
- Principal component analysis: can be applied to the covariance matrix square root in Monte-Carlo simulations, or to "compress" large baskets, as well as for portfolio risk.
While it sounds like a straightforward remark, I have found that people (including myself) tend to do the same mistakes in finance. We might use some quadrature, find out it does not perform that well in some cases, replace it with another one that behaves a bit better, without investigating the real issue: why does the first quadrature break? is the new quadrature really fixing the issue?
Machine Learning & Quantitative Finance
There is an interesting course on Machine Learning on Coursera, it does not require much knowledge and yet manages to teach quite a lot.
I was struck by the fact that most techniques and ideas apply also to problems in quantitative finance.
While it sounds like a straightforward remark, I have found that people (including myself) tend to do the same mistakes in finance. We might use some quadrature, find out it does not perform that well in some cases, replace it with another one that behaves a bit better, without investigating the real issue: why does the first quadrature break? is the new quadrature really fixing the issue?
I was struck by the fact that most techniques and ideas apply also to problems in quantitative finance.
- Linear regression: used for example in the Longstaff-Schwartz approach to price Bermudan options with Monte-Carlo. Interestingly the teacher insists on feature normalization, something we can forget easily, especially with the polynomial features.
- Gradient descent: one of the most basic minimizer and we use minimizers all the time for model calibration.
- Regularization: in finance, this is sometimes used to smooth out the volatility surface, or can be useful to add stability in calibration. The lessons are very practical, they explain well how to find the right value of the regularization parameter.
- Neural networks: calibrating a model is very much like training a neural network. The backpropagation is the same thing as the adjoint differentiation. It's very interesting to see that it is a key feature for Neural networks, otherwise training would be much too slow and Neural networks would not be practical. Once the network is trained, it is evaluated relatively quickly forward. It's basically the same thing as calibration and then pricing.
- Support vector machines: A gaussian kernel is often used to represent the frontier. We find the same idea in the particle Monte-Carlo method.
- Principal component analysis: can be applied to the covariance matrix square root in Monte-Carlo simulations, or to "compress" large baskets, as well as for portfolio risk.
While it sounds like a straightforward remark, I have found that people (including myself) tend to do the same mistakes in finance. We might use some quadrature, find out it does not perform that well in some cases, replace it with another one that behaves a bit better, without investigating the real issue: why does the first quadrature break? is the new quadrature really fixing the issue?
Wednesday, November 12, 2014
Pseudo-Random vs Quasi-Random Numbers
Quasi-Random numbers (like Sobol) are a relatively popular way in finance to improve the Monte-Carlo convergence compared to more classic Pseudo-Random numbers (like Mersenne-Twister). Behind the scenes one has to be a bit more careful about the dimension of the problem as the Quasi-Random numbers depends on the dimension (defined by how many random variables are independent from each other).
For a long time, Sobol was limited to 40 dimensions using the so called Bratley-Fox direction numbers (his paper actually gives the numbers for 50 dimensions). Later Lemieux gave direction numbers for up to 360 dimensions. Then, P. Jäckel proposed some extension with a random initialization of the direction vectors in his book from 2006. And finally Joe & Kuo published direction numbers for up to 21200 dimensions.
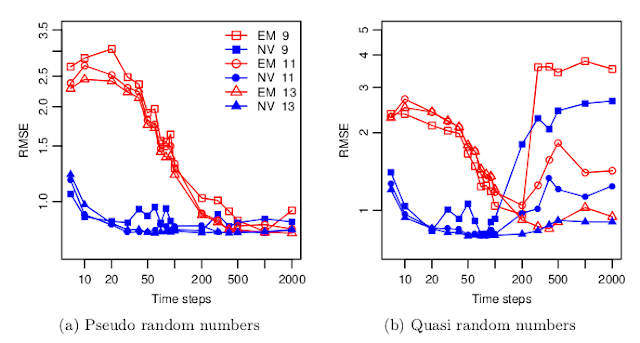
But there are very few studies about how good are real world simulations with so many quasi-random dimensions. A recent paper "Fast Ninomiya-Victoir Calibration of the Double-Mean-Reverting Model" by Bayer, Gatheral & Karlsmark tests this for once, and the results are not so pretty:
With their model, the convergence with Sobol numbers becomes worse when the number of time-steps increases, that is when the number of dimension increases. There seems to be even a threshold around 100 time steps (=300 dimensions for Euler) beyond which a much higher number of paths (2^13) is necessary to restore a proper convergence. And they use the latest and greatest Joe-Kuo direction numbers.
Still the total number of paths is not that high compared to what I am usually using (2^13 = 8192). It's an interesting aspect of their paper: the calibration with a low number of paths.
For a long time, Sobol was limited to 40 dimensions using the so called Bratley-Fox direction numbers (his paper actually gives the numbers for 50 dimensions). Later Lemieux gave direction numbers for up to 360 dimensions. Then, P. Jäckel proposed some extension with a random initialization of the direction vectors in his book from 2006. And finally Joe & Kuo published direction numbers for up to 21200 dimensions.
But there are very few studies about how good are real world simulations with so many quasi-random dimensions. A recent paper "Fast Ninomiya-Victoir Calibration of the Double-Mean-Reverting Model" by Bayer, Gatheral & Karlsmark tests this for once, and the results are not so pretty:
With their model, the convergence with Sobol numbers becomes worse when the number of time-steps increases, that is when the number of dimension increases. There seems to be even a threshold around 100 time steps (=300 dimensions for Euler) beyond which a much higher number of paths (2^13) is necessary to restore a proper convergence. And they use the latest and greatest Joe-Kuo direction numbers.
Still the total number of paths is not that high compared to what I am usually using (2^13 = 8192). It's an interesting aspect of their paper: the calibration with a low number of paths.
Pseudo-Random vs Quasi-Random Numbers
Quasi-Random numbers (like Sobol) are a relatively popular way in finance to improve the Monte-Carlo convergence compared to more classic Pseudo-Random numbers (like Mersenne-Twister). Behind the scenes one has to be a bit more careful about the dimension of the problem as the Quasi-Random numbers depends on the dimension (defined by how many random variables are independent from each other).
For a long time, Sobol was limited to 40 dimensions using the so called Bratley-Fox direction numbers (his paper actually gives the numbers for 50 dimensions). Later Lemieux gave direction numbers for up to 360 dimensions. Then, P. Jäckel proposed some extension with a random initialization of the direction vectors in his book from 2006. And finally Joe & Kuo published direction numbers for up to 21200 dimensions.
But there are very few studies about how good are real world simulations with so many quasi-random dimensions. A recent paper "Fast Ninomiya-Victoir Calibration of the Double-Mean-Reverting Model" by Bayer, Gatheral & Karlsmark tests this for once, and the results are not so pretty:
With their model, the convergence with Sobol numbers becomes worse when the number of time-steps increases, that is when the number of dimension increases. There seems to be even a threshold around 100 time steps (=300 dimensions for Euler) beyond which a much higher number of paths (2^13) is necessary to restore a proper convergence. And they use the latest and greatest Joe-Kuo direction numbers.
Still the total number of paths is not that high compared to what I am usually using (2^13 = 8192). It's an interesting aspect of their paper: the calibration with a low number of paths.
For a long time, Sobol was limited to 40 dimensions using the so called Bratley-Fox direction numbers (his paper actually gives the numbers for 50 dimensions). Later Lemieux gave direction numbers for up to 360 dimensions. Then, P. Jäckel proposed some extension with a random initialization of the direction vectors in his book from 2006. And finally Joe & Kuo published direction numbers for up to 21200 dimensions.
But there are very few studies about how good are real world simulations with so many quasi-random dimensions. A recent paper "Fast Ninomiya-Victoir Calibration of the Double-Mean-Reverting Model" by Bayer, Gatheral & Karlsmark tests this for once, and the results are not so pretty:
With their model, the convergence with Sobol numbers becomes worse when the number of time-steps increases, that is when the number of dimension increases. There seems to be even a threshold around 100 time steps (=300 dimensions for Euler) beyond which a much higher number of paths (2^13) is necessary to restore a proper convergence. And they use the latest and greatest Joe-Kuo direction numbers.
Still the total number of paths is not that high compared to what I am usually using (2^13 = 8192). It's an interesting aspect of their paper: the calibration with a low number of paths.
Wednesday, November 05, 2014
Integrating an oscillatory function
Recently, some instabilities were noticed in the Carr-Lee seasoned volatility swap price in some situations.
The Carr-Lee seasoned volatility swap price involve the computation of a double integral. The inner integral is really the problematic one as the integrand can be highly oscillating.

I first found a somewhat stable behavior using a specific adaptive Gauss-Lobatto implementation (the one from Espelid) and a change of variable. But it was not very satisfying to see that the outer integral was stable only with another specific adaptive Gauss-Lobatto (the one from Gander & Gauschi, present in Quantlib). I tried various choices of adaptive (coteda, modsim, adaptsim,...) or brute force trapezoidal integration, but either they were order of magnitudes slower or unstable in some cases. Just using the same Gauss-Lobatto implementation for both would fail...
I then noticed you could write the integral as a Fourier transform as well, allowing the use of FFT. Unfortunately, while this worked, it turned out to require a very large number of points for a reasonable accuracy. This, plus the tricky part of defining the proper step size, makes the method not so practical.
I had heard before of the Filon quadrature, which I thought was more of a curiosity. The main idea is to integrate exactly x^n * cos(k*x). One then relies on a piecewise parabolic approximation of the function f to integrate f(x) * cos(k*x). Interestingly, a very similar idea has been used in the Sali quadrature method for option pricing, except one integrates exactly x^n * exp(-k*x^2).
It turned out to be remarkable on that problem, combined with a simple adaptive Simpson like method to find the right discretization. Then as if by magic, any outer integration quadrature worked.
The Carr-Lee seasoned volatility swap price involve the computation of a double integral. The inner integral is really the problematic one as the integrand can be highly oscillating.

I first found a somewhat stable behavior using a specific adaptive Gauss-Lobatto implementation (the one from Espelid) and a change of variable. But it was not very satisfying to see that the outer integral was stable only with another specific adaptive Gauss-Lobatto (the one from Gander & Gauschi, present in Quantlib). I tried various choices of adaptive (coteda, modsim, adaptsim,...) or brute force trapezoidal integration, but either they were order of magnitudes slower or unstable in some cases. Just using the same Gauss-Lobatto implementation for both would fail...
I then noticed you could write the integral as a Fourier transform as well, allowing the use of FFT. Unfortunately, while this worked, it turned out to require a very large number of points for a reasonable accuracy. This, plus the tricky part of defining the proper step size, makes the method not so practical.
I had heard before of the Filon quadrature, which I thought was more of a curiosity. The main idea is to integrate exactly x^n * cos(k*x). One then relies on a piecewise parabolic approximation of the function f to integrate f(x) * cos(k*x). Interestingly, a very similar idea has been used in the Sali quadrature method for option pricing, except one integrates exactly x^n * exp(-k*x^2).
It turned out to be remarkable on that problem, combined with a simple adaptive Simpson like method to find the right discretization. Then as if by magic, any outer integration quadrature worked.
Integrating an oscillatory function
Recently, some instabilities were noticed in the Carr-Lee seasoned volatility swap price in some situations.
The Carr-Lee seasoned volatility swap price involve the computation of a double integral. The inner integral is really the problematic one as the integrand can be highly oscillating.

I first found a somewhat stable behavior using a specific adaptive Gauss-Lobatto implementation (the one from Espelid) and a change of variable. But it was not very satisfying to see that the outer integral was stable only with another specific adaptive Gauss-Lobatto (the one from Gander & Gauschi, present in Quantlib). I tried various choices of adaptive (coteda, modsim, adaptsim,...) or brute force trapezoidal integration, but either they were order of magnitudes slower or unstable in some cases. Just using the same Gauss-Lobatto implementation for both would fail...
I then noticed you could write the integral as a Fourier transform as well, allowing the use of FFT. Unfortunately, while this worked, it turned out to require a very large number of points for a reasonable accuracy. This, plus the tricky part of defining the proper step size, makes the method not so practical.
I had heard before of the Filon quadrature, which I thought was more of a curiosity. The main idea is to integrate exactly x^n * cos(k*x). One then relies on a piecewise parabolic approximation of the function f to integrate f(x) * cos(k*x). Interestingly, a very similar idea has been used in the Sali quadrature method for option pricing, except one integrates exactly x^n * exp(-k*x^2).
It turned out to be remarkable on that problem, combined with a simple adaptive Simpson like method to find the right discretization. Then as if by magic, any outer integration quadrature worked.
The Carr-Lee seasoned volatility swap price involve the computation of a double integral. The inner integral is really the problematic one as the integrand can be highly oscillating.

I first found a somewhat stable behavior using a specific adaptive Gauss-Lobatto implementation (the one from Espelid) and a change of variable. But it was not very satisfying to see that the outer integral was stable only with another specific adaptive Gauss-Lobatto (the one from Gander & Gauschi, present in Quantlib). I tried various choices of adaptive (coteda, modsim, adaptsim,...) or brute force trapezoidal integration, but either they were order of magnitudes slower or unstable in some cases. Just using the same Gauss-Lobatto implementation for both would fail...
I then noticed you could write the integral as a Fourier transform as well, allowing the use of FFT. Unfortunately, while this worked, it turned out to require a very large number of points for a reasonable accuracy. This, plus the tricky part of defining the proper step size, makes the method not so practical.
I had heard before of the Filon quadrature, which I thought was more of a curiosity. The main idea is to integrate exactly x^n * cos(k*x). One then relies on a piecewise parabolic approximation of the function f to integrate f(x) * cos(k*x). Interestingly, a very similar idea has been used in the Sali quadrature method for option pricing, except one integrates exactly x^n * exp(-k*x^2).
It turned out to be remarkable on that problem, combined with a simple adaptive Simpson like method to find the right discretization. Then as if by magic, any outer integration quadrature worked.
Monday, November 03, 2014
The elusive reference: the Lamperti transform
Without knowing that it was a well known general concept, I first noticed the use of the Lamperti transform in the Andersen-Piterbarg "Interest rate modeling" book p292 "finite difference solutions for general phi".
Pat Hagan used that transformation for a better discretization of the arbitrage free SABR PDE model.
I then started to notice the use of this transformation in many more papers. The first one I saw naming it "Lamperti transform" was the paper from Ait-Sahalia "Maximum likelyhood estimation of discretely sampled diffusions: a closed-form approximation approach". Recently those closed form formulae have been applied to the quadrature method (where one integrates the transition density by a quadrature rule) in "Advancing the universality of quadrature methods to any underlying process for option pricing". There is also a recent interesting application to Monte-Carlo simulation in "Unbiased Estimation with Square Root Convergence for SDE Models".
So the range of practical applications is quite large. But there was still no reference. A google search pointed me to a well written paper that describes the application of the Lamperti transform to various stochastic differential equations, showing its limits "From State Dependent Diffusion to Constant Diffusion in Stochastic Differential Equations by the Lamperti Transform".
Gary then blogged about the Lamperti transform and various papers from Lamperti, but does not say which one is the source.
After going through some, I noticed that Lamperti's 1964 "A simple construction of certain diffusion processes" seemed to be the closest, even though it seems to go beyond stochastic differential equations.
Today, I found a paper referencing this paper explicitly when presenting the transformation of a stochastic process to a unit diffusion in "Density estimates for solutions to one dimensional Backward SDE's". In addition it also references one exercise of the Karatzas-Schreve book "Brownian motion and Stochastic calculus", which presents again the same idea, without calling it Lamperti transform.
The elusive reference: the Lamperti transform
Without knowing that it was a well known general concept, I first noticed the use of the Lamperti transform in the Andersen-Piterbarg "Interest rate modeling" book p292 "finite difference solutions for general phi".
Pat Hagan used that transformation for a better discretization of the arbitrage free SABR PDE model.
I then started to notice the use of this transformation in many more papers. The first one I saw naming it "Lamperti transform" was the paper from Ait-Sahalia "Maximum likelyhood estimation of discretely sampled diffusions: a closed-form approximation approach". Recently those closed form formulae have been applied to the quadrature method (where one integrates the transition density by a quadrature rule) in "Advancing the universality of quadrature methods to any underlying process for option pricing". There is also a recent interesting application to Monte-Carlo simulation in "Unbiased Estimation with Square Root Convergence for SDE Models".
So the range of practical applications is quite large. But there was still no reference. A google search pointed me to a well written paper that describes the application of the Lamperti transform to various stochastic differential equations, showing its limits "From State Dependent Diffusion to Constant Diffusion in Stochastic Differential Equations by the Lamperti Transform".
Gary then blogged about the Lamperti transform and various papers from Lamperti, but does not say which one is the source.
After going through some, I noticed that Lamperti's 1964 "A simple construction of certain diffusion processes" seemed to be the closest, even though it seems to go beyond stochastic differential equations.
Today, I found a paper referencing this paper explicitly when presenting the transformation of a stochastic process to a unit diffusion in "Density estimates for solutions to one dimensional Backward SDE's". In addition it also references one exercise of the Karatzas-Schreve book "Brownian motion and Stochastic calculus", which presents again the same idea, without calling it Lamperti transform.
Thursday, October 02, 2014
Barrier options under negative rates: complex numbers to the rescue
I stumbled upon an unexpected problem: the one touch barrier formula can break down under negative rates. While negative rates can sound fancy, they are actually quite real on some markets. Combined with relatively low volatilities, this makes the standard Black-Scholes one touch barrier formula blow up because somewhere the square root of a negative number is taken.
At first, I had the idea to just floor the number to 0. But then I needed to see if this rough approximation would be acceptable or not. So I relied on a TR-BDF2 discretization of the Black-Scholes PDE, where negative rates are not a problem.
Later, I was convinced that we ought to be able to find a closed form formula for the case of negative rates. I went back to the derivation of the formula, the book from Kwok is quite good on that. The closed form formula just stems from being the solution of an integral of the first passage time density (which is a simpler way to compute the one touch price than the PDE approach). It turns out that, then, the closed form solution to this integral with negative rates is just the same formula with complex numbers (there are actually some simplifications then).
It is a bit uncommon to use the cumulative normal distribution on complex numbers, but the error function on complex numbers is more popular: it's actually even on the wikipedia page of the error function. And it can be computed very quickly with machine precision thanks to the Faddeeva library.
With this simple closed form formula, there is no need anymore for an approximation. I wrote a small paper around this here.
Later a collegue made the remark that it could be interesting to have the bivariate complex normal distribution for the case of partial start one touch options or partial barrier option rebates (not sure if those are common). Unfortunately I could not find any code or paper for this. And after asking Prof. Genz (who found a very elegant and fast algorithm for the bivariate normal distribution), it looks like an open problem.
At first, I had the idea to just floor the number to 0. But then I needed to see if this rough approximation would be acceptable or not. So I relied on a TR-BDF2 discretization of the Black-Scholes PDE, where negative rates are not a problem.
Later, I was convinced that we ought to be able to find a closed form formula for the case of negative rates. I went back to the derivation of the formula, the book from Kwok is quite good on that. The closed form formula just stems from being the solution of an integral of the first passage time density (which is a simpler way to compute the one touch price than the PDE approach). It turns out that, then, the closed form solution to this integral with negative rates is just the same formula with complex numbers (there are actually some simplifications then).
It is a bit uncommon to use the cumulative normal distribution on complex numbers, but the error function on complex numbers is more popular: it's actually even on the wikipedia page of the error function. And it can be computed very quickly with machine precision thanks to the Faddeeva library.
With this simple closed form formula, there is no need anymore for an approximation. I wrote a small paper around this here.
Later a collegue made the remark that it could be interesting to have the bivariate complex normal distribution for the case of partial start one touch options or partial barrier option rebates (not sure if those are common). Unfortunately I could not find any code or paper for this. And after asking Prof. Genz (who found a very elegant and fast algorithm for the bivariate normal distribution), it looks like an open problem.
Barrier options under negative rates: complex numbers to the rescue
I stumbled upon an unexpected problem: the one touch barrier formula can break down under negative rates. While negative rates can sound fancy, they are actually quite real on some markets. Combined with relatively low volatilities, this makes the standard Black-Scholes one touch barrier formula blow up because somewhere the square root of a negative number is taken.
At first, I had the idea to just floor the number to 0. But then I needed to see if this rough approximation would be acceptable or not. So I relied on a TR-BDF2 discretization of the Black-Scholes PDE, where negative rates are not a problem.
Later, I was convinced that we ought to be able to find a closed form formula for the case of negative rates. I went back to the derivation of the formula, the book from Kwok is quite good on that. The closed form formula just stems from being the solution of an integral of the first passage time density (which is a simpler way to compute the one touch price than the PDE approach). It turns out that, then, the closed form solution to this integral with negative rates is just the same formula with complex numbers (there are actually some simplifications then).
It is a bit uncommon to use the cumulative normal distribution on complex numbers, but the error function on complex numbers is more popular: it's actually even on the wikipedia page of the error function. And it can be computed very quickly with machine precision thanks to the Faddeeva library.
With this simple closed form formula, there is no need anymore for an approximation. I wrote a small paper around this here.
Later a collegue made the remark that it could be interesting to have the bivariate complex normal distribution for the case of partial start one touch options or partial barrier option rebates (not sure if those are common). Unfortunately I could not find any code or paper for this. And after asking Prof. Genz (who found a very elegant and fast algorithm for the bivariate normal distribution), it looks like an open problem.
At first, I had the idea to just floor the number to 0. But then I needed to see if this rough approximation would be acceptable or not. So I relied on a TR-BDF2 discretization of the Black-Scholes PDE, where negative rates are not a problem.
Later, I was convinced that we ought to be able to find a closed form formula for the case of negative rates. I went back to the derivation of the formula, the book from Kwok is quite good on that. The closed form formula just stems from being the solution of an integral of the first passage time density (which is a simpler way to compute the one touch price than the PDE approach). It turns out that, then, the closed form solution to this integral with negative rates is just the same formula with complex numbers (there are actually some simplifications then).
It is a bit uncommon to use the cumulative normal distribution on complex numbers, but the error function on complex numbers is more popular: it's actually even on the wikipedia page of the error function. And it can be computed very quickly with machine precision thanks to the Faddeeva library.
With this simple closed form formula, there is no need anymore for an approximation. I wrote a small paper around this here.
Later a collegue made the remark that it could be interesting to have the bivariate complex normal distribution for the case of partial start one touch options or partial barrier option rebates (not sure if those are common). Unfortunately I could not find any code or paper for this. And after asking Prof. Genz (who found a very elegant and fast algorithm for the bivariate normal distribution), it looks like an open problem.
Friday, September 26, 2014
Initial Guesses for SVI - A Summary
I have been looking at various ways of finding initial guesses for SVI calibration (Another SVI Initial Guess, More SVI Initial Guesses, SVI and long maturities issues). I decided to write a paper summarizing this. I find that the process of writing a paper makes me think more carefully about a problem.
In this case, it turns out that the Vogt initial guess method (guess via asymptotes and minimum variance) is actually very good as long as one has a good way to lookup the asymptotes (the data is not always convex, while SVI is) and as long as rho is not close to -1, that is for long maturity affine like smiles, where SVI is actually more difficult to calibrate properly due to the over-parameterisation in those cases.
Still after looking at all of this, one has a sense that, even though it works on a wide variety of surfaces, it could break down because of the complexity (are asymptotes ok, is rho close to -1? how close? is ATM better or maximum curvature better? how do we impose boundaries on a and sigma with Levenberg-Marquardt? (truncation should not be too close to the transform, but how far?)
This is where the Quasi-Explicit method from Zeliade is very interesting: it is simpler, not necessarily to code, but the method itself. There are things to take care of (solving at each boundary), but those are mathematically well defined. The only drawback is performance, as it can be around 40 times slower. But then it's still not that slow.
In this case, it turns out that the Vogt initial guess method (guess via asymptotes and minimum variance) is actually very good as long as one has a good way to lookup the asymptotes (the data is not always convex, while SVI is) and as long as rho is not close to -1, that is for long maturity affine like smiles, where SVI is actually more difficult to calibrate properly due to the over-parameterisation in those cases.
Still after looking at all of this, one has a sense that, even though it works on a wide variety of surfaces, it could break down because of the complexity (are asymptotes ok, is rho close to -1? how close? is ATM better or maximum curvature better? how do we impose boundaries on a and sigma with Levenberg-Marquardt? (truncation should not be too close to the transform, but how far?)
This is where the Quasi-Explicit method from Zeliade is very interesting: it is simpler, not necessarily to code, but the method itself. There are things to take care of (solving at each boundary), but those are mathematically well defined. The only drawback is performance, as it can be around 40 times slower. But then it's still not that slow.
Initial Guesses for SVI - A Summary
I have been looking at various ways of finding initial guesses for SVI calibration (Another SVI Initial Guess, More SVI Initial Guesses, SVI and long maturities issues). I decided to write a paper summarizing this. I find that the process of writing a paper makes me think more carefully about a problem.
In this case, it turns out that the Vogt initial guess method (guess via asymptotes and minimum variance) is actually very good as long as one has a good way to lookup the asymptotes (the data is not always convex, while SVI is) and as long as rho is not close to -1, that is for long maturity affine like smiles, where SVI is actually more difficult to calibrate properly due to the over-parameterisation in those cases.
Still after looking at all of this, one has a sense that, even though it works on a wide variety of surfaces, it could break down because of the complexity (are asymptotes ok, is rho close to -1? how close? is ATM better or maximum curvature better? how do we impose boundaries on a and sigma with Levenberg-Marquardt? (truncation should not be too close to the transform, but how far?)
This is where the Quasi-Explicit method from Zeliade is very interesting: it is simpler, not necessarily to code, but the method itself. There are things to take care of (solving at each boundary), but those are mathematically well defined. The only drawback is performance, as it can be around 40 times slower. But then it's still not that slow.
In this case, it turns out that the Vogt initial guess method (guess via asymptotes and minimum variance) is actually very good as long as one has a good way to lookup the asymptotes (the data is not always convex, while SVI is) and as long as rho is not close to -1, that is for long maturity affine like smiles, where SVI is actually more difficult to calibrate properly due to the over-parameterisation in those cases.
Still after looking at all of this, one has a sense that, even though it works on a wide variety of surfaces, it could break down because of the complexity (are asymptotes ok, is rho close to -1? how close? is ATM better or maximum curvature better? how do we impose boundaries on a and sigma with Levenberg-Marquardt? (truncation should not be too close to the transform, but how far?)
This is where the Quasi-Explicit method from Zeliade is very interesting: it is simpler, not necessarily to code, but the method itself. There are things to take care of (solving at each boundary), but those are mathematically well defined. The only drawback is performance, as it can be around 40 times slower. But then it's still not that slow.
Tuesday, September 23, 2014
Asymptotic Behavior of SVI vs SABR
The variance under SVI becomes linear when the log-moneyness is very large in absolute terms. The lognormal SABR formula with beta=0 or beta=1 has a very different behavior. Of course, the theoretical SABR model has actually a different asymptotic behavior.
As an illustration, we calibrate SABR (with two different values of beta) and SVI against the same implied volatility slice and look at the wings behavior.
While the Lee moments formula implies that the variance should be at most linear, something that the SABR formula does not respect. It is in practice not the problem with SABR as the actual Lee boundary: V(x) < 2|x|/T (where V is the square of the implied volatility and x the log-moneyness) is attained for extremely low strikes only with SABR, except maybe for very long maturities.
A related behavior is the fact that the lognormal SABR formula can actually match steeper curvatures at the money than SVI for given asymptotes.
As an illustration, we calibrate SABR (with two different values of beta) and SVI against the same implied volatility slice and look at the wings behavior.
While the Lee moments formula implies that the variance should be at most linear, something that the SABR formula does not respect. It is in practice not the problem with SABR as the actual Lee boundary: V(x) < 2|x|/T (where V is the square of the implied volatility and x the log-moneyness) is attained for extremely low strikes only with SABR, except maybe for very long maturities.
A related behavior is the fact that the lognormal SABR formula can actually match steeper curvatures at the money than SVI for given asymptotes.
Asymptotic Behavior of SVI vs SABR
The variance under SVI becomes linear when the log-moneyness is very large in absolute terms. The lognormal SABR formula with beta=0 or beta=1 has a very different behavior. Of course, the theoretical SABR model has actually a different asymptotic behavior.
As an illustration, we calibrate SABR (with two different values of beta) and SVI against the same implied volatility slice and look at the wings behavior.
While the Lee moments formula implies that the variance should be at most linear, something that the SABR formula does not respect. It is in practice not the problem with SABR as the actual Lee boundary: V(x) < 2|x|/T (where V is the square of the implied volatility and x the log-moneyness) is attained for extremely low strikes only with SABR, except maybe for very long maturities.
A related behavior is the fact that the lognormal SABR formula can actually match steeper curvatures at the money than SVI for given asymptotes.
As an illustration, we calibrate SABR (with two different values of beta) and SVI against the same implied volatility slice and look at the wings behavior.
While the Lee moments formula implies that the variance should be at most linear, something that the SABR formula does not respect. It is in practice not the problem with SABR as the actual Lee boundary: V(x) < 2|x|/T (where V is the square of the implied volatility and x the log-moneyness) is attained for extremely low strikes only with SABR, except maybe for very long maturities.
A related behavior is the fact that the lognormal SABR formula can actually match steeper curvatures at the money than SVI for given asymptotes.
Friday, August 01, 2014
SVI and long maturities issues
On long maturities equity options, the smile is usually very much like a skew: very little curvature. This usually means that the SVI rho will be very close to -1, in a similar fashion as what can happen for the the correlation parameter of a real stochastic volatility model (Heston, SABR).
In terms of initial guess, we looked at the more usual use cases and showed that matching a parabola at the minimum variance point often leads to a decent initial guess if one has an ok estimate of the wings. We will see here that we can do also something a bit better than just a flat slice at-the-money in the case where rho is close to -1.
In general when the asymptotes lead to rho < -1, it means that we can't compute b from the asymptotes as there is in reality only one usable asymptote, the other one having a slope of 0 (rho=-1). The right way is to just recompute b by matching the ATM slope (which can be estimated by fitting a parabola at the money). Then we can try to match the ATM curvature, there are two possibilities to simplify the problem: s >> m or m >> s.
Interestingly, there is some kind of discontinuity at m = 0:
This apparently simple issue is actually a core problem with SVI. Looking back at our slopes but this time in the moneyness coordinate, the slope at m is b*rho while the slope at the money is b*(rho-1) if m != 0. If s is small, as the curvature at m is just b/s this means that our there will always be this funny shape if s is small. It seems then that the best we can do is hide it: let m>max(moneyness) and compute the sigma to match the ATM curvature. This leads to the following:
This is all good so far. Unfortunately running a minimizer on it will lead to a solution with a small s. And the bigger picture looks like this (QE is Zeliade Quasi-Explicit, Levenberg-Marquardt would give the same result):
Of course a simple fix is to not let s to be too small, but how do we defined what is too small? I have found that a simple rule is too always ensure that s is increasing with the maturity supposing that we have to fit a surface. This rule has also a very nice side effect that spurious arbitrages will tend to disappear as well. On the figure above, I can bet that there is a big arbitrage at k=m for the QE result.
In terms of initial guess, we looked at the more usual use cases and showed that matching a parabola at the minimum variance point often leads to a decent initial guess if one has an ok estimate of the wings. We will see here that we can do also something a bit better than just a flat slice at-the-money in the case where rho is close to -1.
In general when the asymptotes lead to rho < -1, it means that we can't compute b from the asymptotes as there is in reality only one usable asymptote, the other one having a slope of 0 (rho=-1). The right way is to just recompute b by matching the ATM slope (which can be estimated by fitting a parabola at the money). Then we can try to match the ATM curvature, there are two possibilities to simplify the problem: s >> m or m >> s.
Interestingly, there is some kind of discontinuity at m = 0:
- when m = 0, the at-the-money slope is just b*rho.
- when m != 0 and m >> s, the at-the-money slope is b*(rho-1).
This apparently simple issue is actually a core problem with SVI. Looking back at our slopes but this time in the moneyness coordinate, the slope at m is b*rho while the slope at the money is b*(rho-1) if m != 0. If s is small, as the curvature at m is just b/s this means that our there will always be this funny shape if s is small. It seems then that the best we can do is hide it: let m>max(moneyness) and compute the sigma to match the ATM curvature. This leads to the following:
This is all good so far. Unfortunately running a minimizer on it will lead to a solution with a small s. And the bigger picture looks like this (QE is Zeliade Quasi-Explicit, Levenberg-Marquardt would give the same result):
Of course a simple fix is to not let s to be too small, but how do we defined what is too small? I have found that a simple rule is too always ensure that s is increasing with the maturity supposing that we have to fit a surface. This rule has also a very nice side effect that spurious arbitrages will tend to disappear as well. On the figure above, I can bet that there is a big arbitrage at k=m for the QE result.
SVI and long maturities issues
On long maturities equity options, the smile is usually very much like a skew: very little curvature. This usually means that the SVI rho will be very close to -1, in a similar fashion as what can happen for the the correlation parameter of a real stochastic volatility model (Heston, SABR).
In terms of initial guess, we looked at the more usual use cases and showed that matching a parabola at the minimum variance point often leads to a decent initial guess if one has an ok estimate of the wings. We will see here that we can do also something a bit better than just a flat slice at-the-money in the case where rho is close to -1.
In general when the asymptotes lead to rho < -1, it means that we can't compute b from the asymptotes as there is in reality only one usable asymptote, the other one having a slope of 0 (rho=-1). The right way is to just recompute b by matching the ATM slope (which can be estimated by fitting a parabola at the money). Then we can try to match the ATM curvature, there are two possibilities to simplify the problem: s >> m or m >> s.
Interestingly, there is some kind of discontinuity at m = 0:
This apparently simple issue is actually a core problem with SVI. Looking back at our slopes but this time in the moneyness coordinate, the slope at m is b*rho while the slope at the money is b*(rho-1) if m != 0. If s is small, as the curvature at m is just b/s this means that our there will always be this funny shape if s is small. It seems then that the best we can do is hide it: let m>max(moneyness) and compute the sigma to match the ATM curvature. This leads to the following:
This is all good so far. Unfortunately running a minimizer on it will lead to a solution with a small s. And the bigger picture looks like this (QE is Zeliade Quasi-Explicit, Levenberg-Marquardt would give the same result):
Of course a simple fix is to not let s to be too small, but how do we defined what is too small? I have found that a simple rule is too always ensure that s is increasing with the maturity supposing that we have to fit a surface. This rule has also a very nice side effect that spurious arbitrages will tend to disappear as well. On the figure above, I can bet that there is a big arbitrage at k=m for the QE result.
In terms of initial guess, we looked at the more usual use cases and showed that matching a parabola at the minimum variance point often leads to a decent initial guess if one has an ok estimate of the wings. We will see here that we can do also something a bit better than just a flat slice at-the-money in the case where rho is close to -1.
In general when the asymptotes lead to rho < -1, it means that we can't compute b from the asymptotes as there is in reality only one usable asymptote, the other one having a slope of 0 (rho=-1). The right way is to just recompute b by matching the ATM slope (which can be estimated by fitting a parabola at the money). Then we can try to match the ATM curvature, there are two possibilities to simplify the problem: s >> m or m >> s.
Interestingly, there is some kind of discontinuity at m = 0:
- when m = 0, the at-the-money slope is just b*rho.
- when m != 0 and m >> s, the at-the-money slope is b*(rho-1).
This apparently simple issue is actually a core problem with SVI. Looking back at our slopes but this time in the moneyness coordinate, the slope at m is b*rho while the slope at the money is b*(rho-1) if m != 0. If s is small, as the curvature at m is just b/s this means that our there will always be this funny shape if s is small. It seems then that the best we can do is hide it: let m>max(moneyness) and compute the sigma to match the ATM curvature. This leads to the following:
This is all good so far. Unfortunately running a minimizer on it will lead to a solution with a small s. And the bigger picture looks like this (QE is Zeliade Quasi-Explicit, Levenberg-Marquardt would give the same result):
Of course a simple fix is to not let s to be too small, but how do we defined what is too small? I have found that a simple rule is too always ensure that s is increasing with the maturity supposing that we have to fit a surface. This rule has also a very nice side effect that spurious arbitrages will tend to disappear as well. On the figure above, I can bet that there is a big arbitrage at k=m for the QE result.
Thursday, July 31, 2014
More SVI Initial Guesses
In the previous post, I showed one could extract the SVI parameters from a best fit parabola at-the-money. It seemed to work reasonably well, but I found some real market data where it can be much less satisfying.
Sometimes (actually not so rarely) the ATM slope and curvatures can't be matched given rho and b found through the asymptotes. As a result if I force to just match the curvature and set m=0 (when the slope can't be matched), the simple ATM parabolic guess looks shifted. It can be much worse than this specific example.
It is then a bit clearer why Vogt looked to match the lowest variance instead of ATM. We can actually also fit a parabola at the lowest variance (MV suffix in the graph) instead of ATM. It seems to fit generally better.
I also tried to estimate the asymptotic slopes more precisely (using the slope of the 5-points parabola at each end), but it seems to not always be an improvement.
However this does not work when rho is close to -1 or 1 as there is then no minimum. Often, matching ATM also does not work when rho is -1 or 1. This specific case, but quite common as well for longer expiries in equities need more thoughts, usually a constant slice is ok, but this is clearly where Zeliade's quasi explicit method shines.
So far it still all looks good, but then looking at medium maturities (1 year), sometimes all initial guesses don't look comforting (although Levenberg-Marquardt minimization still works on those - but one can easily imagine that it can break as well, for example by tweaking slightly the rho/b and look at what happens then).
There is lots of data on this 1 year example. One can clearly see the problem when the slope can not be fitted ATM (SimpleParabolicATM-guess), and even if by chance when it can (TripleParabolicATM-guess), it's not so great.
Similarly fitting the lowest variance leads only to a good fit of the right wing and a bad fit everywhere else.
Still, as if by miracle, everything converges to the best fit on this example (again one can find cases where some guesses don't converge to the best fit). I have added some weights +-20% around the money, to ensure that we capture the ATM behavior accurately (otherwise the best fit is funny).
It is interesting to see that if one minimizes the min square sum of variances (what I do in Vogt-LM, it's in theory slightly faster as there is no sqrt function cost) it results in an ugly looking steeper curvature, while if we just minimize the min square sum of volatilities (what I do in SimpleParabolicMV_LM), it looks better.
Sometimes (actually not so rarely) the ATM slope and curvatures can't be matched given rho and b found through the asymptotes. As a result if I force to just match the curvature and set m=0 (when the slope can't be matched), the simple ATM parabolic guess looks shifted. It can be much worse than this specific example.
It is then a bit clearer why Vogt looked to match the lowest variance instead of ATM. We can actually also fit a parabola at the lowest variance (MV suffix in the graph) instead of ATM. It seems to fit generally better.
I also tried to estimate the asymptotic slopes more precisely (using the slope of the 5-points parabola at each end), but it seems to not always be an improvement.
However this does not work when rho is close to -1 or 1 as there is then no minimum. Often, matching ATM also does not work when rho is -1 or 1. This specific case, but quite common as well for longer expiries in equities need more thoughts, usually a constant slice is ok, but this is clearly where Zeliade's quasi explicit method shines.
So far it still all looks good, but then looking at medium maturities (1 year), sometimes all initial guesses don't look comforting (although Levenberg-Marquardt minimization still works on those - but one can easily imagine that it can break as well, for example by tweaking slightly the rho/b and look at what happens then).
There is lots of data on this 1 year example. One can clearly see the problem when the slope can not be fitted ATM (SimpleParabolicATM-guess), and even if by chance when it can (TripleParabolicATM-guess), it's not so great.
Similarly fitting the lowest variance leads only to a good fit of the right wing and a bad fit everywhere else.
Still, as if by miracle, everything converges to the best fit on this example (again one can find cases where some guesses don't converge to the best fit). I have added some weights +-20% around the money, to ensure that we capture the ATM behavior accurately (otherwise the best fit is funny).
It is interesting to see that if one minimizes the min square sum of variances (what I do in Vogt-LM, it's in theory slightly faster as there is no sqrt function cost) it results in an ugly looking steeper curvature, while if we just minimize the min square sum of volatilities (what I do in SimpleParabolicMV_LM), it looks better.
More SVI Initial Guesses
In the previous post, I showed one could extract the SVI parameters from a best fit parabola at-the-money. It seemed to work reasonably well, but I found some real market data where it can be much less satisfying.
Sometimes (actually not so rarely) the ATM slope and curvatures can't be matched given rho and b found through the asymptotes. As a result if I force to just match the curvature and set m=0 (when the slope can't be matched), the simple ATM parabolic guess looks shifted. It can be much worse than this specific example.
It is then a bit clearer why Vogt looked to match the lowest variance instead of ATM. We can actually also fit a parabola at the lowest variance (MV suffix in the graph) instead of ATM. It seems to fit generally better.
I also tried to estimate the asymptotic slopes more precisely (using the slope of the 5-points parabola at each end), but it seems to not always be an improvement.
However this does not work when rho is close to -1 or 1 as there is then no minimum. Often, matching ATM also does not work when rho is -1 or 1. This specific case, but quite common as well for longer expiries in equities need more thoughts, usually a constant slice is ok, but this is clearly where Zeliade's quasi explicit method shines.
So far it still all looks good, but then looking at medium maturities (1 year), sometimes all initial guesses don't look comforting (although Levenberg-Marquardt minimization still works on those - but one can easily imagine that it can break as well, for example by tweaking slightly the rho/b and look at what happens then).
There is lots of data on this 1 year example. One can clearly see the problem when the slope can not be fitted ATM (SimpleParabolicATM-guess), and even if by chance when it can (TripleParabolicATM-guess), it's not so great.
Similarly fitting the lowest variance leads only to a good fit of the right wing and a bad fit everywhere else.
Still, as if by miracle, everything converges to the best fit on this example (again one can find cases where some guesses don't converge to the best fit). I have added some weights +-20% around the money, to ensure that we capture the ATM behavior accurately (otherwise the best fit is funny).
It is interesting to see that if one minimizes the min square sum of variances (what I do in Vogt-LM, it's in theory slightly faster as there is no sqrt function cost) it results in an ugly looking steeper curvature, while if we just minimize the min square sum of volatilities (what I do in SimpleParabolicMV_LM), it looks better.
It is then a bit clearer why Vogt looked to match the lowest variance instead of ATM. We can actually also fit a parabola at the lowest variance (MV suffix in the graph) instead of ATM. It seems to fit generally better.
I also tried to estimate the asymptotic slopes more precisely (using the slope of the 5-points parabola at each end), but it seems to not always be an improvement.
However this does not work when rho is close to -1 or 1 as there is then no minimum. Often, matching ATM also does not work when rho is -1 or 1. This specific case, but quite common as well for longer expiries in equities need more thoughts, usually a constant slice is ok, but this is clearly where Zeliade's quasi explicit method shines.
So far it still all looks good, but then looking at medium maturities (1 year), sometimes all initial guesses don't look comforting (although Levenberg-Marquardt minimization still works on those - but one can easily imagine that it can break as well, for example by tweaking slightly the rho/b and look at what happens then).
Similarly fitting the lowest variance leads only to a good fit of the right wing and a bad fit everywhere else.
Still, as if by miracle, everything converges to the best fit on this example (again one can find cases where some guesses don't converge to the best fit). I have added some weights +-20% around the money, to ensure that we capture the ATM behavior accurately (otherwise the best fit is funny).
It is interesting to see that if one minimizes the min square sum of variances (what I do in Vogt-LM, it's in theory slightly faster as there is no sqrt function cost) it results in an ugly looking steeper curvature, while if we just minimize the min square sum of volatilities (what I do in SimpleParabolicMV_LM), it looks better.
Tuesday, July 29, 2014
Another SVI Initial Guess
The SVI formula is:
$$w(k) = a + b ( \rho (k-m) + \sqrt{(k-m)^2+ \sigma^2}$$
where k is the log-moneyness, w(k) the implied variance at a given moneyness and a,b,rho,m,sigma the 5 SVI parameters.
A. Vogt described a particularly simple way to find an initial guess to fit SVI to an implied volatility slice a while ago. The idea to compute rho and sigma from the left and right asymptotic slopes. a,m are recovered from the crossing point of the asymptotes and sigma using the minimum variance.
Later, Zeliade has shown a very nice reduction of the problem to 2 variables, while the remaining 3 can be deduced explicitly. The practical side is that constraints are automatically included, the less practical side is the choice of minimizer for the two variables (Nelder-Mead) and of initial guess (a few random points).
Instead, a simple alternative is the following: given b and rho from the asymptotic slopes, one could also just fit a parabola at-the-money, in a similar spirit as the explicit SABR calibration, and recover explicitly a, m and sigma.
To illustrate I take the data from Zeliade, where the input is already some SVI fit to market data.
We clearly see that ATM the fit is better for the parabolic initial guess than for Vogt, but as one goes further away from ATM, Vogt guess seems better.
Compared to SABR, the parabola itself fits decently only very close to ATM. If one computes the higher order Taylor expansion of SVI around k=0, powers of (k/sigma) appear, while sigma is often relatively small especially for short expiries: the fourth derivative will quickly make a difference.
On implied volatilities stemming from a SABR fit of the SP500, here is how the various methods behave:
As expected, because SABR (and thus the input implied vol) is much closer to a parabola, the parabolic initial guess is much better than Vogt. The initial guess of Vogt is particularly bad on long expiries, although it will still converge quite quickly to the true minimum with Levenberg-Marquardt.
In practice, I have found the method of Zeliade to be very robust, even if a bit slower than Vogt, while Vogt can sometimes (rarely) be too sensitive to the estimate of the asymptotes.
The parabolic guess method could also be applied to always fit exactly ATM vol, slope and curvature, and calibrate rho, b to gives the best overall fit. It might be an idea for the next blog post.
$$w(k) = a + b ( \rho (k-m) + \sqrt{(k-m)^2+ \sigma^2}$$
where k is the log-moneyness, w(k) the implied variance at a given moneyness and a,b,rho,m,sigma the 5 SVI parameters.
A. Vogt described a particularly simple way to find an initial guess to fit SVI to an implied volatility slice a while ago. The idea to compute rho and sigma from the left and right asymptotic slopes. a,m are recovered from the crossing point of the asymptotes and sigma using the minimum variance.
Later, Zeliade has shown a very nice reduction of the problem to 2 variables, while the remaining 3 can be deduced explicitly. The practical side is that constraints are automatically included, the less practical side is the choice of minimizer for the two variables (Nelder-Mead) and of initial guess (a few random points).
Instead, a simple alternative is the following: given b and rho from the asymptotic slopes, one could also just fit a parabola at-the-money, in a similar spirit as the explicit SABR calibration, and recover explicitly a, m and sigma.
To illustrate I take the data from Zeliade, where the input is already some SVI fit to market data.
 |
| 3M expiry - Zeliade data |
 |
| 4Y expiry, Zeliade data |
Compared to SABR, the parabola itself fits decently only very close to ATM. If one computes the higher order Taylor expansion of SVI around k=0, powers of (k/sigma) appear, while sigma is often relatively small especially for short expiries: the fourth derivative will quickly make a difference.
On implied volatilities stemming from a SABR fit of the SP500, here is how the various methods behave:
 |
| 1M expiry on SABR data |
 |
| 4Y expiry on SABR data |
In practice, I have found the method of Zeliade to be very robust, even if a bit slower than Vogt, while Vogt can sometimes (rarely) be too sensitive to the estimate of the asymptotes.
The parabolic guess method could also be applied to always fit exactly ATM vol, slope and curvature, and calibrate rho, b to gives the best overall fit. It might be an idea for the next blog post.
Another SVI Initial Guess
The SVI formula is:
$$w(k) = a + b ( \rho (k-m) + \sqrt{(k-m)^2+ \sigma^2}$$
where k is the log-moneyness, w(k) the implied variance at a given moneyness and a,b,rho,m,sigma the 5 SVI parameters.
A. Vogt described a particularly simple way to find an initial guess to fit SVI to an implied volatility slice a while ago. The idea to compute rho and sigma from the left and right asymptotic slopes. a,m are recovered from the crossing point of the asymptotes and sigma using the minimum variance.
Later, Zeliade has shown a very nice reduction of the problem to 2 variables, while the remaining 3 can be deduced explicitly. The practical side is that constraints are automatically included, the less practical side is the choice of minimizer for the two variables (Nelder-Mead) and of initial guess (a few random points).
Instead, a simple alternative is the following: given b and rho from the asymptotic slopes, one could also just fit a parabola at-the-money, in a similar spirit as the explicit SABR calibration, and recover explicitly a, m and sigma.
To illustrate I take the data from Zeliade, where the input is already some SVI fit to market data.
We clearly see that ATM the fit is better for the parabolic initial guess than for Vogt, but as one goes further away from ATM, Vogt guess seems better.
Compared to SABR, the parabola itself fits decently only very close to ATM. If one computes the higher order Taylor expansion of SVI around k=0, powers of (k/sigma) appear, while sigma is often relatively small especially for short expiries: the fourth derivative will quickly make a difference.
On implied volatilities stemming from a SABR fit of the SP500, here is how the various methods behave:
As expected, because SABR (and thus the input implied vol) is much closer to a parabola, the parabolic initial guess is much better than Vogt. The initial guess of Vogt is particularly bad on long expiries, although it will still converge quite quickly to the true minimum with Levenberg-Marquardt.
In practice, I have found the method of Zeliade to be very robust, even if a bit slower than Vogt, while Vogt can sometimes (rarely) be too sensitive to the estimate of the asymptotes.
The parabolic guess method could also be applied to always fit exactly ATM vol, slope and curvature, and calibrate rho, b to gives the best overall fit. It might be an idea for the next blog post.
$$w(k) = a + b ( \rho (k-m) + \sqrt{(k-m)^2+ \sigma^2}$$
where k is the log-moneyness, w(k) the implied variance at a given moneyness and a,b,rho,m,sigma the 5 SVI parameters.
A. Vogt described a particularly simple way to find an initial guess to fit SVI to an implied volatility slice a while ago. The idea to compute rho and sigma from the left and right asymptotic slopes. a,m are recovered from the crossing point of the asymptotes and sigma using the minimum variance.
Later, Zeliade has shown a very nice reduction of the problem to 2 variables, while the remaining 3 can be deduced explicitly. The practical side is that constraints are automatically included, the less practical side is the choice of minimizer for the two variables (Nelder-Mead) and of initial guess (a few random points).
Instead, a simple alternative is the following: given b and rho from the asymptotic slopes, one could also just fit a parabola at-the-money, in a similar spirit as the explicit SABR calibration, and recover explicitly a, m and sigma.
To illustrate I take the data from Zeliade, where the input is already some SVI fit to market data.
 |
| 3M expiry - Zeliade data |
 |
| 4Y expiry, Zeliade data |
Compared to SABR, the parabola itself fits decently only very close to ATM. If one computes the higher order Taylor expansion of SVI around k=0, powers of (k/sigma) appear, while sigma is often relatively small especially for short expiries: the fourth derivative will quickly make a difference.
On implied volatilities stemming from a SABR fit of the SP500, here is how the various methods behave:
 |
| 1M expiry on SABR data |
 |
| 4Y expiry on SABR data |
In practice, I have found the method of Zeliade to be very robust, even if a bit slower than Vogt, while Vogt can sometimes (rarely) be too sensitive to the estimate of the asymptotes.
The parabolic guess method could also be applied to always fit exactly ATM vol, slope and curvature, and calibrate rho, b to gives the best overall fit. It might be an idea for the next blog post.
Wednesday, July 16, 2014
New SABR Formulae
In a talk at the Global Derivatives conference of Amsterdam (2014), Pat Hagan presented some new SABR formulas, supposedly close to the arbitrage free PDE behavior.
I tried to code those from the slides, but somehow that did not work out well on his example, I just had something very close to the good old SABR formulas. I am not 100% sure (only 99%) that it is due to a mistake in my code. Here is what I was looking to reproduce:
Fortunately, I then found in some thesis the idea of using Andersen & Brotherton-Ratcliffe local volatility expansion. In deed, the arbitrage free PDE from Hagan is equivalent to some Dupire local volatility forward PDE (see http://papers.ssrn.com/abstract=2402001), so Hagan just gave us the local volatility expansion to expand on (the thesis uses Doust, which is not so different in this case).
And then it produces on this global derivatives example the following:
The AB suffix are the new SABR formula. Even though the formulas are different, that looks very much like Hagan's own illustration (with a better scale)!
I have a draft paper around this and more practical ideas to calibrate SABR:
http://papers.ssrn.com/abstract=2467231
I tried to code those from the slides, but somehow that did not work out well on his example, I just had something very close to the good old SABR formulas. I am not 100% sure (only 99%) that it is due to a mistake in my code. Here is what I was looking to reproduce:
 |
| Pat Hagan Global Derivatives example |
Fortunately, I then found in some thesis the idea of using Andersen & Brotherton-Ratcliffe local volatility expansion. In deed, the arbitrage free PDE from Hagan is equivalent to some Dupire local volatility forward PDE (see http://papers.ssrn.com/abstract=2402001), so Hagan just gave us the local volatility expansion to expand on (the thesis uses Doust, which is not so different in this case).
And then it produces on this global derivatives example the following:
The AB suffix are the new SABR formula. Even though the formulas are different, that looks very much like Hagan's own illustration (with a better scale)!
I have a draft paper around this and more practical ideas to calibrate SABR:
http://papers.ssrn.com/abstract=2467231
New SABR Formulae
In a talk at the Global Derivatives conference of Amsterdam (2014), Pat Hagan presented some new SABR formulas, supposedly close to the arbitrage free PDE behavior.
I tried to code those from the slides, but somehow that did not work out well on his example, I just had something very close to the good old SABR formulas. I am not 100% sure (only 99%) that it is due to a mistake in my code. Here is what I was looking to reproduce:
Fortunately, I then found in some thesis the idea of using Andersen & Brotherton-Ratcliffe local volatility expansion. In deed, the arbitrage free PDE from Hagan is equivalent to some Dupire local volatility forward PDE (see http://papers.ssrn.com/abstract=2402001), so Hagan just gave us the local volatility expansion to expand on (the thesis uses Doust, which is not so different in this case).
And then it produces on this global derivatives example the following:
The AB suffix are the new SABR formula. Even though the formulas are different, that looks very much like Hagan's own illustration (with a better scale)!
I have a draft paper around this and more practical ideas to calibrate SABR:
http://papers.ssrn.com/abstract=2467231
I tried to code those from the slides, but somehow that did not work out well on his example, I just had something very close to the good old SABR formulas. I am not 100% sure (only 99%) that it is due to a mistake in my code. Here is what I was looking to reproduce:
 |
| Pat Hagan Global Derivatives example |
Fortunately, I then found in some thesis the idea of using Andersen & Brotherton-Ratcliffe local volatility expansion. In deed, the arbitrage free PDE from Hagan is equivalent to some Dupire local volatility forward PDE (see http://papers.ssrn.com/abstract=2402001), so Hagan just gave us the local volatility expansion to expand on (the thesis uses Doust, which is not so different in this case).
And then it produces on this global derivatives example the following:
The AB suffix are the new SABR formula. Even though the formulas are different, that looks very much like Hagan's own illustration (with a better scale)!
I have a draft paper around this and more practical ideas to calibrate SABR:
http://papers.ssrn.com/abstract=2467231
Thursday, July 03, 2014
Heston or Schobel-Zhu issues with short expiries
It's relatively well known that Heston does not fit the market for short expiries. Given that there are just 5 parameters to fit a full surface, it's almost logical that one part of the surface of it is not going to fit well the market.
I was more surprised to see how bad Heston or Schobel-Zhu were to fit a single short expiry volatility slice. As an example I looked at SP500 options with 1 week expiry. It does not really matter if one forces kappa and rho to constant values (even to 0) the behavior is the same and the error in fit does not change much.
In this graph, the brown, green and red smiles corresponds to Schobel-Zhu fit using an explicit guess (matching skew & curvature ATM), using Levenberg-Marquardt on this guess, and using plain differential evolution.
What happens is that the smiles flattens to quickly in the strike dimension. One consequence is that the implied volatility can not be computed for extreme strikes: the smile being too low, the price becomes extremely small, under machine epsilon and the numerical method (Cos) fails. There is also a bogus angle in the right wing, because of numerical error. I paid attention to ignore too small prices in the calibration by truncating the initial data.
SABR behaves much better (fixing beta=1 in this case) in comparison (As I use the same truncation as for Schobel-Zhu, the flat left wing part is ignored).
For longer expiries, Heston & Schobel-Zhu, even limited to 3 parameters, actually give a better fit in general than SABR.
I was more surprised to see how bad Heston or Schobel-Zhu were to fit a single short expiry volatility slice. As an example I looked at SP500 options with 1 week expiry. It does not really matter if one forces kappa and rho to constant values (even to 0) the behavior is the same and the error in fit does not change much.
 |
| Schobel-Zhu fit for a slice of maturity 1 week |
What happens is that the smiles flattens to quickly in the strike dimension. One consequence is that the implied volatility can not be computed for extreme strikes: the smile being too low, the price becomes extremely small, under machine epsilon and the numerical method (Cos) fails. There is also a bogus angle in the right wing, because of numerical error. I paid attention to ignore too small prices in the calibration by truncating the initial data.
 |
| Heston fit, with Lord-Kahl (exact wings) |
SABR behaves much better (fixing beta=1 in this case) in comparison (As I use the same truncation as for Schobel-Zhu, the flat left wing part is ignored).
 |
| SABR fit for a slice of maturity 1 week |
Heston or Schobel-Zhu issues with short expiries
It's relatively well known that Heston does not fit the market for short expiries. Given that there are just 5 parameters to fit a full surface, it's almost logical that one part of the surface of it is not going to fit well the market.
I was more surprised to see how bad Heston or Schobel-Zhu were to fit a single short expiry volatility slice. As an example I looked at SP500 options with 1 week expiry. It does not really matter if one forces kappa and rho to constant values (even to 0) the behavior is the same and the error in fit does not change much.
In this graph, the brown, green and red smiles corresponds to Schobel-Zhu fit using an explicit guess (matching skew & curvature ATM), using Levenberg-Marquardt on this guess, and using plain differential evolution.
What happens is that the smiles flattens to quickly in the strike dimension. One consequence is that the implied volatility can not be computed for extreme strikes: the smile being too low, the price becomes extremely small, under machine epsilon and the numerical method (Cos) fails. There is also a bogus angle in the right wing, because of numerical error. I paid attention to ignore too small prices in the calibration by truncating the initial data.
SABR behaves much better (fixing beta=1 in this case) in comparison (As I use the same truncation as for Schobel-Zhu, the flat left wing part is ignored).
For longer expiries, Heston & Schobel-Zhu, even limited to 3 parameters, actually give a better fit in general than SABR.
I was more surprised to see how bad Heston or Schobel-Zhu were to fit a single short expiry volatility slice. As an example I looked at SP500 options with 1 week expiry. It does not really matter if one forces kappa and rho to constant values (even to 0) the behavior is the same and the error in fit does not change much.
 |
| Schobel-Zhu fit for a slice of maturity 1 week |
What happens is that the smiles flattens to quickly in the strike dimension. One consequence is that the implied volatility can not be computed for extreme strikes: the smile being too low, the price becomes extremely small, under machine epsilon and the numerical method (Cos) fails. There is also a bogus angle in the right wing, because of numerical error. I paid attention to ignore too small prices in the calibration by truncating the initial data.
 |
| Heston fit, with Lord-Kahl (exact wings) |
SABR behaves much better (fixing beta=1 in this case) in comparison (As I use the same truncation as for Schobel-Zhu, the flat left wing part is ignored).
 |
| SABR fit for a slice of maturity 1 week |
Sunday, June 29, 2014
On the Role of Static Types and Generic Types on Productivity
Most developers have strong opinions on dynamic types programming languages vs static types programming languages. The former is often assumed to be good for small projects/prototyping while the later better for bigger projects. But there is a surprisingly small number of studies to back those claims.
One such study is "An experiment about static and dynamic type systems: doubts about the positive impact of static type systems on development time" and came to the conclusion that on a small project, static typing did not decrease programming time, and actually increased debugging time. However 4 years later, "An empirical comparison of static and dynamic type systems on API usage in the presence of an IDE: Java vs. groovy with eclipse" shows that a developer is 2x more productive with Java than with Groovy using an unknown API. This contrasts a bit (but does not contradict) with their previous study "Static Type Systems (Sometimes) have a Positive Impact on the Usability of Undocumented Software: An Empirical Evaluation" that showed Groovy to be more productive on small projects. One problem is that all these studies stem from the same person.
It's more interesting to look at generic types vs raw types use, where even less studies have been done. "Do developers benefit from generic types?: an empirical comparison of generic and raw types in java" concludes that generic types do not provide any advantages to fix typing errors, hardly surprising in my opinion. Generic types (especially with type erasure as in Java) is the typical idea that sounds good but that in practice does not really help: it makes the code actually more awkward to read and tend to make developers too lazy to create new classes that would often be more appropriate than a generic type (think Map<String,List<Map<String, Date>>>).
One such study is "An experiment about static and dynamic type systems: doubts about the positive impact of static type systems on development time" and came to the conclusion that on a small project, static typing did not decrease programming time, and actually increased debugging time. However 4 years later, "An empirical comparison of static and dynamic type systems on API usage in the presence of an IDE: Java vs. groovy with eclipse" shows that a developer is 2x more productive with Java than with Groovy using an unknown API. This contrasts a bit (but does not contradict) with their previous study "Static Type Systems (Sometimes) have a Positive Impact on the Usability of Undocumented Software: An Empirical Evaluation" that showed Groovy to be more productive on small projects. One problem is that all these studies stem from the same person.
It's more interesting to look at generic types vs raw types use, where even less studies have been done. "Do developers benefit from generic types?: an empirical comparison of generic and raw types in java" concludes that generic types do not provide any advantages to fix typing errors, hardly surprising in my opinion. Generic types (especially with type erasure as in Java) is the typical idea that sounds good but that in practice does not really help: it makes the code actually more awkward to read and tend to make developers too lazy to create new classes that would often be more appropriate than a generic type (think Map<String,List<Map<String, Date>>>).
Subscribe to:
Posts
(
Atom
)